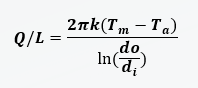Comparison of Heat Loss Calculation Methods - through Datasheet & through Equation
Which one is better - method introduced in Chromalox, or IEEE 515?
In this article, I’ll compare two ways to calculate the heat loss, compare pros and cons of each method, and give my opinion which one is better.
Way from Chromalox Design Guide Book
When I entered EHT industry, I started to learn heat loss calculation method through Chromalox Design Guide Book. The equation to calculate the heat loss for pipe was as below.
Equation to calculate heat loss per length
Q = Qp × △T × 2(KTm + KTa)
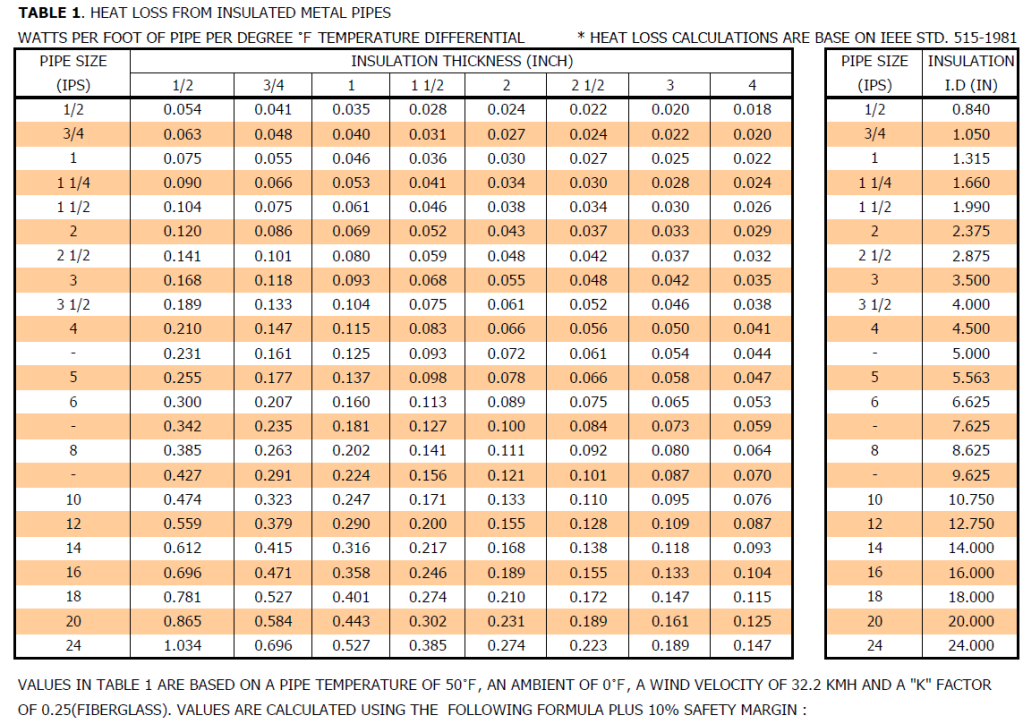
Find Qp in below table according to the given pipe size and insulation thickness.
(For example, Qp value of 3" pipe with 2" would be 0.055)
Multiply by temperature difference △T, which is (maintain temperature - min. ambient temperature).
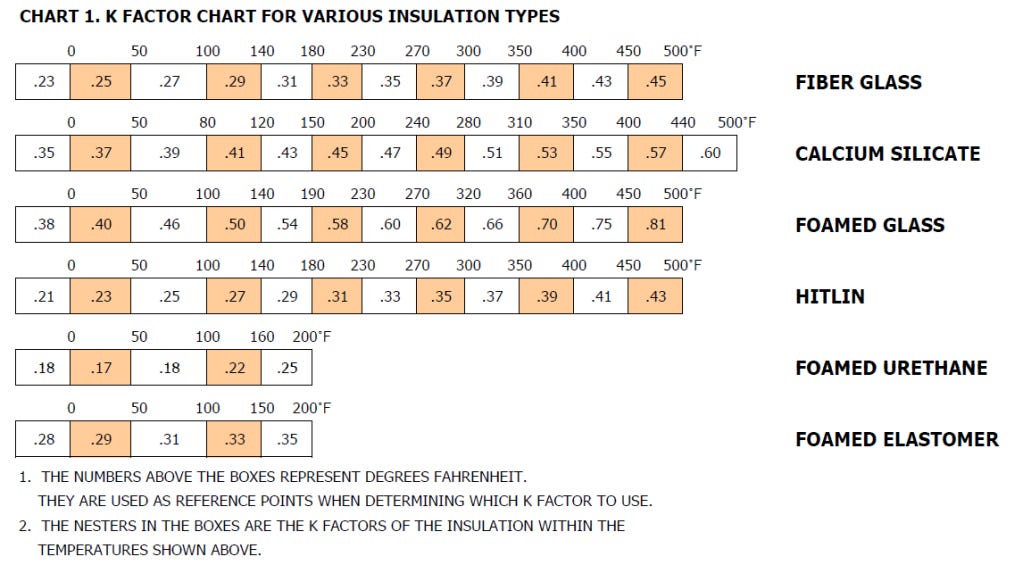
Depending on the maintain temperature and minimum ambient temperature for specific material, KTM and KTa values are decided according to below table.
I have used above method for years.
But first of all, I was not satisfied of converting Celsius to Fahrenheit, and meter to foot. After the calculation, I need to convert to metric values again. I thought ‘Why should I do conversion every time when I do the calculation?’
In addition, though I have to find values in the table, but the table displays only standard values. It means if my data is not mentioned in the table, I have to estimate with the similar values which could make the possible incorrect values.
I wondered whether calculation on the Chromalox design guide book was only way. When I searched on IEEE 515 document which is standard for the EHT engineering, I was surprised that the calculation method is pretty much different from my previous knowledge.
Way from IEEE 515 Document
Q = Heat transfer rate (W)
L = Pipe (cylinder) length (m)
Q/L = Heat transfer rate per length (W/m)
k = Thermal conductivity of insulation material (W/m∙K)
Tm= Maintain temperature (℃)
Ta= Ambient temperature (℃)
do= Outer diameter of the insulation (m)
di= Inner diameter of the insulation (m)
It looks complicated, but it was more intuitive.
Q/L is the heat loss value per length which we aim to calculate.
di (inner diameter of the insulation) is same as outer diameter of pipe, assuming that there is no air layer between the insulation and pipe. As the pipe size is given by nominal size in inch, we should check the outer diameter in metric dimension.
Nominal Pipe size(inch) → Outside Diameter(mm)
⅛ → 10.3 / ¼ → 13.7 / ⅜ → 17.1 / ½ → 21.3 / ¾ → 26.7 / 1 '' → 33.4 / 1¼ → 42.2
1½ → 48.3 / 2 '' → 60.3 / 2½ → 73 / 3 '' → 88.9 / 3½ → 101.6 / 4 '' → 114.3 / 5 '' → 141.3
6 '' → 168.3 / 8 '' → 219.1 / 10 '' → 273.1 / 12 '' → 323.9 / 14 '' → 355.6
16 '' → 406.4 / 18 '' → 457 / 20 ''→ 508
Assuming that there is no air layer, do (outer diameter of insulation) = di + insulation thickness
Thermal conductivity k value depends on the insulation material. Below are k values for representative insulation materials.
Insulation → K (W/m ℃)
Mineral Wool → 0.047 / Rockwool → 0.037 / Fiber Glass → 0.038 / Cellulose → 0.04
Polyurethane Foam → 0.03 / Polystyrene → 0.033 / Aerogel → 0.02
Chromalox method may be easier at the beginning, as we do not need to know the concept of nominal pipe size and thermal conductivity. But considering that IEEE method can calculate the heat loss value in any given condition, I’d choose to use the IEEE method.